Números racionais e irracionais são dois conceitos fundamentais na matemática, e compreender suas diferenças e aplicações é essencial para a resolução de problemas em diversas áreas do conhecimento.
Embora esses termos sejam frequentemente mencionados em cálculos, muitas pessoas ainda têm dificuldades em entender as distinções entre eles.
Neste post, vamos explorar em detalhes o que são números racionais e irracionais, como podemos identificá-los, quais são suas diferenças e quando devemos usá-los.
Através de exemplos práticos e explicações claras, nosso objetivo é tornar esses conceitos acessíveis e úteis para todos, permitindo uma compreensão mais profunda das suas aplicações na vida cotidiana e nas ciências.
Se você sempre se perguntou quais são os números racionais e irracionais, qual a diferença entre um número racional e um número irracional ou como utilizá-los corretamente, este artigo é para você.
Vamos, então, entender como essas duas categorias de números são fundamentais para a matemática e o impacto que têm no nosso dia a dia.
Matricule seu filho no curso do Kumon e incentive-o a aprender e aplicar matemática no dia a dia. Saiba mais aqui!
Leia mais:
O que são números racionais?
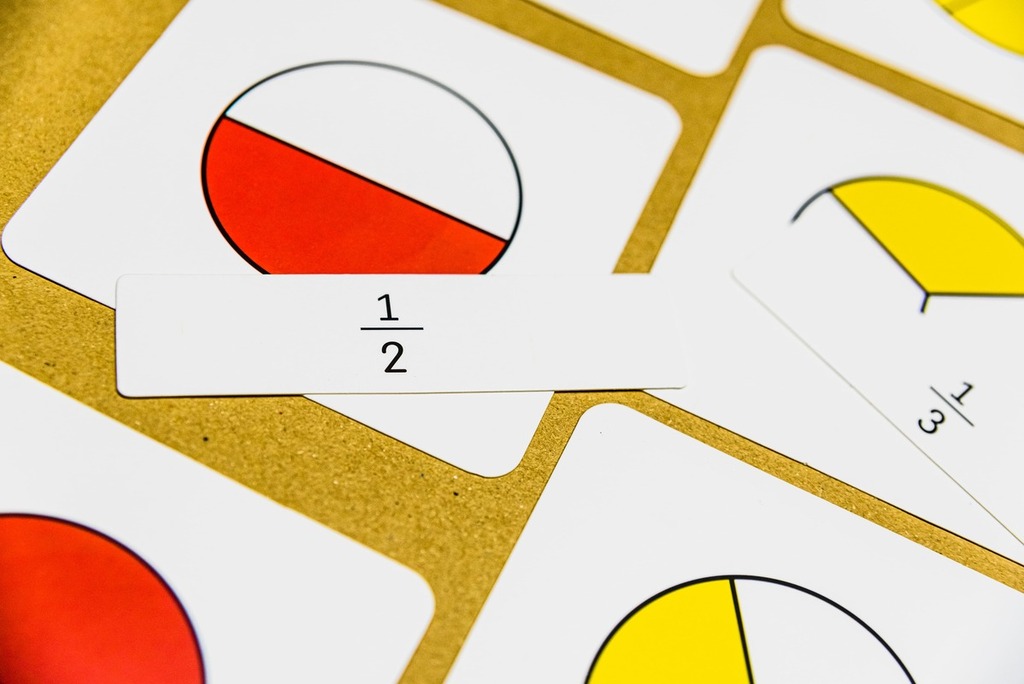
Os números racionais são aqueles que podem ser representados como uma fração a/b, onde a e b são inteiros e b#0. Eles incluem todos os números inteiros, as frações e os decimais que podem ser expressos de forma finita ou periódica.
A grande vantagem dos números racionais é que eles podem ser representados com exatidão, o que os torna ideais para situações que exigem precisão.
Os números racionais têm várias formas de representação, como frações simples (2/3, 5/4), números inteiros (1, -3) ou decimais finitos e periódicos (0,75, 0,3333….).
A característica essencial que define um número racional é justamente a possibilidade de expressá-lo como uma fração de inteiros, o que os torna particularmente úteis em cálculos e medições.
Exemplos de números racionais
Para tornar o conceito de números racionais mais claro, vamos explorar alguns exemplos específicos.
– Números inteiros: Os números inteiros, como -5, 0 e 7, são números racionais porque podem ser expressos como frações, como -5/1, 0/1 e 7/1.
– Frações: Frações simples, como ½, 4/5 e 7/3, são números racionais porque podem ser representadas como a divisão de dois inteiros, o que caracteriza os números racionais.
– Decimais finitos: Números como 0,25, 1,5 e 3,75 são exemplos de números racionais porque suas representações decimais são finitas e podem ser expressas como frações. Por exemplo, 0,25 = 25/100 = ¼.
– Decimais periódicos: Números como 0,3333… (que representa 1/3) e 0,6666… (que representa 2/3) são racionais porque a parte decimal se repete infinitamente, mas ainda pode ser expressa como uma fração de inteiros. A periodicidade é uma característica fundamental desses números.
Operações com números racionais
Os números racionais têm a vantagem de serem facilmente manipulados em diversas operações matemáticas, como adição, subtração, multiplicação e divisão.
Para realizar essas operações com frações, basta seguir alguns passos e regras bem definidas. Vamos detalhar as operações mais comuns.
– Adição e subtração: Para somar ou subtrair frações, é necessário encontrar um denominador comum. Por exemplo, se queremos somar ½ e 1/3, primeiro devemos encontrar um denominador comum, que é 6. Assim, transformamos as frações para 3/6 e 2/6, e então somamos: 3/6 + 2/6 = 5/6.
– Multiplicação: Multiplicar frações é uma operação simples. Multiplicamos os numeradores entre si e os denominadores entre si. Por exemplo, 2/3 x 4/5 = 8/15.
– Divisão: Para dividir frações, multiplicamos pelo inverso da segunda fração. Por exemplo, para dividir 3/4 por 2/5, multiplicamos ¾ x 5/2 = 15/8.
O que são números irracionais?
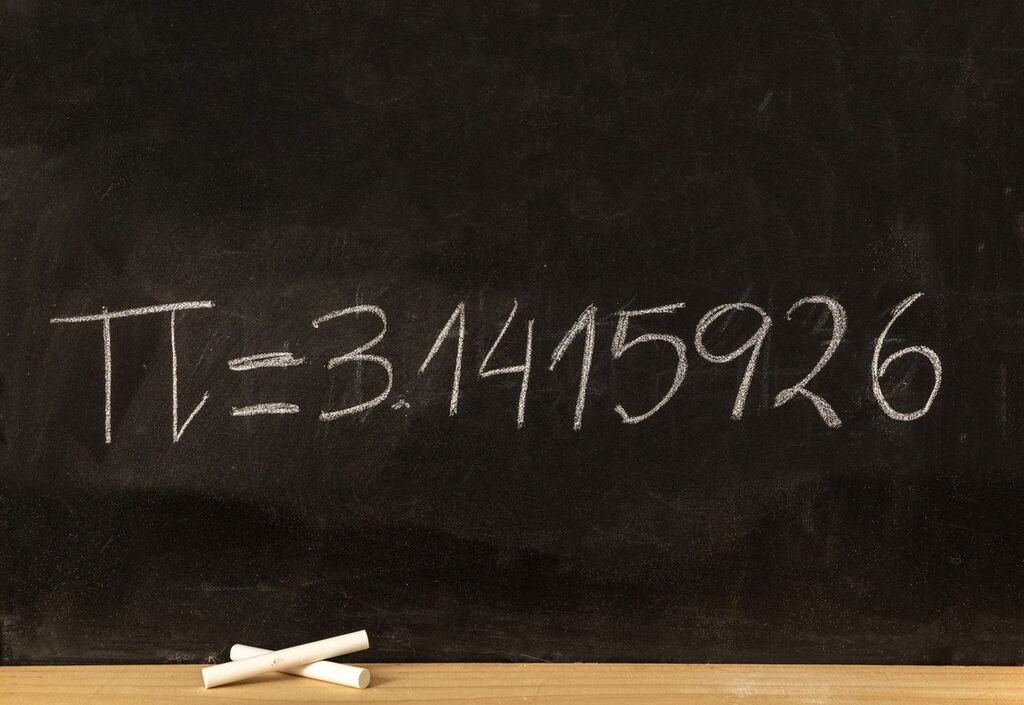
Por outro lado, os números irracionais não podem ser expressos como frações de inteiros. Eles têm uma representação decimal infinita e não periódica, o que significa que seus decimais continuam para sempre sem formar um padrão repetitivo.
Os números irracionais são amplamente utilizados em diversas profissões que usam a matemática, como física, engenharia e matemática avançada, devido à sua capacidade de representar fenômenos naturais e constantes matemáticas que não podem ser descritos de forma exata por números racionais.
Entre os exemplos mais famosos de números irracionais estão o número π (pi), que representa a razão entre a circunferência e o diâmetro de um círculo, e a constante e, usada em cálculos de crescimento exponencial.
Esses números não podem ser representados por frações simples, e suas representações decimais nunca se repetem ou terminam.
Exemplos de números irracionais
A seguir, apresentamos alguns exemplos comuns de números irracionais para facilitar o entendimento:
– Raízes quadradas de números não quadrados perfeitos: Números como √ 2, √ 3 e √ 5 são irracionais, pois suas representações decimais são infinitas e não repetitivas. Por exemplo, √ 2 é aproximadamente 1,41421356…, e esse padrão de decimais nunca se repete.
– O número π: O valor de π é aproximadamente 3,14159…, mas seus decimais continuam infinitamente sem nenhum padrão repetitivo. Este número é amplamente utilizado em cálculos envolvendo círculos e esferas.
– O número e: O número e, bastante utilizado em logaritmos, é uma constante matemática usada para representar o crescimento exponencial. Seu valor é aproximadamente 2,71828…, e, assim como π, seus decimais são infinitos e não periódicos.
Operações com números irracionais
Embora os números irracionais não possam ser manipulados de maneira tão simples quanto os racionais, ainda assim é possível realizar algumas operações com eles. No entanto, o resultado dessas operações geralmente continuará sendo irracional.
– Adição e subtração: Quando somamos ou subtraímos números irracionais, o resultado tende a ser irracional. Por exemplo, π + √ 2 é um número irracional.
– Multiplicação e divisão: Multiplicar ou dividir números irracionais também resulta em números irracionais na maioria das vezes. Por exemplo, π x √ 2 é irracional. Contudo, em alguns casos, a multiplicação ou divisão de números irracionais pode resultar em um número racional, como √ 2 x √ 2 = 2, que é racional.
Embora as operações com números irracionais sejam mais complexas, elas são importantes para a modelagem de fenômenos reais que não podem ser descritos por números racionais.
Números racionais e irracionais: quais as diferenças?
Agora que você já sabe o que são números racionais e irracionais, vamos entender as diferenças entre eles. A principal diferença entre números racionais e irracionais é a sua representação. Os números racionais podem ser expressos como frações a/b, com a e b sendo inteiros e b # 0.
Já os números irracionais não podem ser expressos dessa forma, e suas representações decimais são infinitas e não periódicas.
Essa diferença entre números racionais e irracionais em como cada tipo de número é utilizado em cálculos e problemas matemáticos.
Além disso, enquanto os números racionais são mais comuns em situações cotidianas, como medições precisas e cálculos financeiros, os números irracionais surgem frequentemente em contextos mais avançados, como em modelos científicos e constantes matemáticas.
Como identificar se o número é racional ou irracional?
Identificar se estamos lidando com números racionais e irracionais pode ser feito através de diferentes abordagens, dependendo das informações que você tem sobre o número em questão.
Vamos explorar algumas maneiras de identificar números racionais e irracionais de forma mais detalhada.
Identifique a representação decimal
A forma mais comum de identificar números racionais e irracionais é analisando a sua representação decimal.
A característica essencial dos números racionais em sua forma decimal é que eles podem ter uma representação finita (terminada) ou periódica. Isso significa que a sequência de dígitos após a vírgula se repete de maneira regular em um padrão.
Já os números irracionais não apresentam padrão repetitivo em sua parte decimal. Seus decimais são infinitos e não periódicos, ou seja, não se repetem de forma regular.
Analise as propriedades algébricas
Além das representações decimais e fracionárias, outra maneira de identificar números racionais e irracionais é analisando suas propriedades algébricas. Um número irracional frequentemente surge de operações envolvendo raízes quadradas de números que não são quadrados perfeitos.
De modo geral, números racionais podem ser obtidos a partir de operações algébricas simples envolvendo outros números racionais, como adição, subtração, multiplicação e divisão. Por exemplo, a soma de dois números racionais sempre resultará em outro número racional.
Já para os números irracionais, esse tipo de operação pode gerar resultados que não podem ser expressos como frações. Se você realizar a soma de um número racional com um número irracional, o resultado será sempre irracional.
Da mesma forma, ao multiplicar ou dividir um número racional por um número irracional, o produto ou quociente também será irracional. Isso ocorre porque as propriedades algébricas dos números irracionais impedem que eles se “simplifiquem” para uma forma racional.
Verifique as operações matemáticas
Os números racionais possuem a propriedade de que podem ser manipulados de maneira simples nas operações matemáticas, mantendo-se dentro do conjunto dos números racionais.
Ou seja, se você somar, subtrair, multiplicar ou dividir dois números racionais (desde que a divisão não envolva zero), o resultado sempre será um número racional.
Isso facilita bastante os cálculos e a resolução de problemas matemáticos que envolvem apenas números racionais, uma vez que podemos esperar que todas as operações resultem em números com representação exata.
Por outro lado, ao realizar operações com números irracionais, a situação muda. Quando você soma, subtrai ou multiplica números irracionais, o resultado frequentemente será um número irracional.
Da mesma forma, o produto de dois números irracionais resulta em um número que também não pode ser expresso como uma fração.
Isso reforça a ideia de que, ao lidarmos com números irracionais em operações matemáticas, estamos frequentemente lidando com valores que não podem ser simplificados ou representados de forma exata, o que adiciona complexidade à solução de muitos problemas matemáticos.
Números racionais e irracionais: quando usar?
A compreensão de quais são os números racionais e irracionais e de quando usar números racionais e irracionais é essencial não apenas para o estudo da matemática, mas também para diversas áreas do conhecimento, como ciências, finanças e engenharia.
A aplicação de números racionais e irracionais depende da natureza dos problemas em que estamos trabalhando, e, por isso, entender quando usar cada um deles é importante para garantir precisão e eficácia nos cálculos.
Vamos explorar as situações em que os números racionais e irracionais são mais comuns.
Números racionais
Os números racionais são usados principalmente quando é necessário realizar cálculos precisos e exatos. Exemplos incluem:
– Medidas exatas: Como medir o comprimento de um objeto ou dividir algo em partes iguais.
– Cálculos financeiros: Como calcular juros, prestações e outras operações econômicas.
– Problemas de divisão: Quando se precisa dividir um valor em frações exatas, como em receitas culinárias.
– Cálculos conhecidos: Quando se trabalha com números cujo valor é exato, como ½ ou 3.
Números irracionais
Os números irracionais são mais comumente usados em cálculos que envolvem grande precisão ou que descrevem fenômenos naturais. Exemplos incluem:
– Medições naturais e constantes: Como o valor de π nas fórmulas de círculos e esferas.
– Geometria e trigonometria: Como ao calcular o comprimento de diagonais de quadrados ou o valor de √ 2.
– Modelos matemáticos e físicos: Como em cálculos de crescimento exponencial, usando a constante e.
– Cálculos com precisão infinita: Como em processos contínuos que exigem a precisão extrema dos números irracionais, como a constante "e" e a razão áurea φ.
Conclusão
Números racionais e irracionais são pilares fundamentais da matemática, essenciais para a compreensão e resolução de uma ampla gama de problemas em diversas áreas do conhecimento.
Os números racionais, com suas representações exatas como frações, são perfeitos para situações que demandam precisão finita, como cálculos financeiros, medições exatas e problemas de divisão simples.
Já os números irracionais surgem quando lidamos com constantes naturais, precisões infinitas ou fenômenos complexos, como os encontrados em geometria, trigonometria, física e ciências naturais, onde uma aproximação exata não é possível.
É importante entender o que são números racionais e irracionais. Enquanto os números racionais podem ser expressos de forma simples e clara, os números irracionais trazem consigo a complexidade de uma precisão infinita, mas também a beleza de serem fundamentais para descrever com exatidão muitos dos fenômenos do nosso universo.
A compreensão das características e diferenças entre números racionais e irracionais nos capacita a usar cada um deles de maneira mais eficaz, garantindo que nossas soluções sejam não apenas corretas, mas também aplicáveis à realidade.
Ao dominar quais são os números racionais e irracionais, podemos resolver problemas de maneira mais eficiente e aplicar a matemática de forma mais profunda, seja em problemas cotidianos, seja nas descobertas científicas que nos ajudam a entender melhor o universo.
Sobre o Kumon
O Kumon é um método de estudo que desenvolve ao máximo o potencial do seu filho, de forma individualizada. Criado no Japão em 1958 pelo professor Toru Kumon, o método está presente em mais de 60 países e reúne mais de 4 milhões de estudantes.
Saiba mais
