Frações: o que são, tipos e exemplos para treinar

Você sabia que o aprendizado de matemática do Ensino Médio depende do domínio das frações? Isso quer dizer que, sem aprender de forma consistente este tópico tão importante da matéria, fica muito difícil avançar na compreensão de conteúdos mais avançados.

Portanto, se você quer melhorar seu desempenho em matemática, é fundamental saber mais sobre elas e como funcionam as operações fracionárias. E vamos contar um segredo para você: entender não é tão difícil quanto parece.

Quer uma prova? Então siga em frente com a gente no texto que preparamos sobre este tema que assusta tantos alunos. 

Ao longo do post vamos explicar direitinho quais são os tipos de frações, como fazer operações, dar exemplos com exercícios resolvidos e ajudar você a entender de uma vez este conteúdo!

Aprenda matemática de maneira fácil e prática com o curso do Kumon.

Leia mais:

• Dificuldade em matemática: principais causas e como superá-las

• Estudar para o Enem: como começar e o que estudar para a prova?

• Roteiro de estudos: como montar um que funcione?

O que são frações?

Fração é uma forma de representar uma parte de um todo. Em vez de usar números inteiros, ela mostra quantas partes foram tomadas de algo que foi dividido em partes iguais.

Ou seja, a fração é usada para expressar partes de um inteiro — principalmente quando isso não pode ser representado com números naturais. 

Para ficar mais fácil, vamos pensar no seguinte exemplo: você tem uma barra de chocolate de 8 quadradinhos e quer dividi-la em partes iguais com outra pessoa. 

No final, você vai ficar com 4 quadradinhos e a outra pessoa com 4 também, certo? Ou seja, cada um acaba com 4 partes de 8. Em forma de fração, isso é representado como 4/8.

Porém, no dia a dia, dificilmente diremos que cada pessoa ficou com quatro oitavos da barra. Seria no mínimo esquisito! Então, simplesmente dizemos que cada um comeu metade da barra de chocolate.

Mas digamos que você não seja uma pessoa assim tão justa e igualitária quando o assunto é chocolate, e resolva ficar com 5 quadradinhos e dar apenas 3 para outra pessoa. Neste caso, não há uma palavra comum, como “metade”, para representar essa quantidade.

É aí que entram as frações! Neste exemplo, você ficou com 5/8 da barra, enquanto deu 3/8 para a outra pessoa.

Como as frações são representadas?

A fração nada mais é que a representação de uma divisão. Isto é feito usando um numerador, o algarismo que representa a parte do todo e vem acima, e um denominador, o número que representa o total de partes e vem abaixo.

Viu como é fácil escrever uma fração? A seguir, você vai aprender como ler frações.

Como ler uma fração?

Você vai ver como ler frações é algo simples. Existem algumas regras que valem para todas elas, conforme a tabela abaixo.

Para os números após 9 e aqueles que não são decimais, usamos a palavra “avos”. Por exemplo:

• 9/11 = Nove onze avos

• 11/12 = Onze doze avos

• 19/21 = Dezenove vinte e um avos

Quais são os tipos de frações?

As frações podem ser classificadas em sete tipos: 

• própria

• imprópria

• aparente

• equivalente

• irredutível

• mista

• decimal

Cada uma tem características diferentes, mas todas têm algo em comum: a forma como são estruturadas.

Como vimos, uma fração é composta por duas partes: numerador e denominador.

O numerador — que fica em cima — representa quantas partes estamos considerando. Já o denominador — que fica embaixo — mostra em quantas partes o todo foi dividido.

Voltando ao exemplo do chocolate, dá pra entender bem essa relação se pensarmos na estrutura “numerador – pedaços de – denominador”. No nosso caso, significa que você ficou com 5 pedaços de 8, ou seja, 5/8 da barra.

Mesmo tendo essa mesma estrutura, nem todas as frações são iguais. E entender os tipos de fração faz toda a diferença.

Vamos ver como cada uma funciona?

Fração própria

São frações em que o numerador, ou seja, o pedaço, é menor que o denominador, ou seja, que o todo. As situações que apresentamos acima acima são todas exemplos de frações próprias. 

Veja mais alguns exemplos:

• 1/5

• 2/7

• 11/20

Fração imprópria

Estes tipos de frações são exatamente o contrário das que acabamos de ver. Aqui, o numerador é maior que o denominador. Por exemplo:

• 3/2

• 9/4

• 5/3

Fração aparente

Lembra que dissemos que toda fração representa uma divisão? Em muitos casos, o resultado dessa operação será um número inteiro. Isso acontece quando o numerador é divisível pelo denominador. 

Para ficar mais fácil visualizar, veja estas situações:

• 3/3 = 3 ÷ 3 = 1

• 6/3 = 6 ÷ 3 = 2

• 9/3 = 9 ÷ 3 = 3

Ou seja, sempre que o numerador for um múltiplo exato do denominador, a fração será aparente.

Fração equivalente

Se você dividir uma pizza em dois pedaços e comer um, dividi-la em quatro pedaços e comer dois, ou dividi-la em 8 fatias e comer quatro, no final das contas você terá comido exatamente a mesma quantidade de pizza. 

Assim como neste exemplo, as frações são equivalentes quando representam a mesma parte em relação ao todo. Veja o exemplo da pizza expresso em forma de fração:

• ½ = 2/4 = 4/8

Fração irredutível

Como você acabou de ver, uma mesma quantidade pode ser representada por diferentes frações. Por exemplo: 1/2, 2/4 ou 4/8 expressam a mesma coisa — metade de uma pizza.

Mas entre essas opções, 1/2 é a forma mais simples de representar essa parte. E é justamente isso que chamamos de fração irredutível: a versão mais simples de uma fração.

Para chegar a ela, é necessário que numerador e denominador sejam divididos pelo mesmo número, até que não seja mais possível simplificar.

Vamos a um exemplo:

A fração 18/21 pode ser simplificada. Embora apenas o 18 seja divisível por 2, ambos são divisíveis por 3.

Fazendo essa divisão, temos:

• 18 ÷ 3 = 6

• 21 ÷ 3 = 7

Resultado: 6/7.

Como não existe nenhum outro número, além de 1, que divida os dois ao mesmo tempo, 6/7 é uma fração irredutível.

Ou seja, como o próprio nome diz, é uma fração que não pode mais ser reduzida.

Fração mista

Voltando ao exemplo da pizza: digamos que você estava com muita fome e comeu a pizza inteira. Mas ainda não foi suficiente… então, mandou ver em mais uma fatia de outra pizza que estava dividida em 4 pedaços. 

Mas como representar isso em forma de fração? Com uma fração mista, claro!

As frações mistas são usadas para representar valores que têm uma parte inteira e uma parte fracionária. No exemplo da pizza, você comeu 1 pizza inteira + 1/4 da outra, ou seja: 1 ¼.

Outros exemplos de frações mistas:

• 3 ½

• 5 3/8

• 2 1/6

Elas são super úteis quando queremos expressar quantidades maiores que um, mas com mais clareza do que uma fração imprópria, como 7/4, por exemplo.

Fração decimal

Você provavelmente já viu algo assim no dia a dia: 0,5 litro de água, 2,75 kg de frutas ou 1,25 metros de tecido.

Esses números com vírgula são chamados de números decimais — e, na verdade, também representam frações.

A diferença é que, nesse caso, a fração tem como denominador potências de 10 (ou seja, 10, 100, 1000...).

Vamos a alguns exemplos:

• 0,5 é o mesmo que 5/10.

• 0,25 equivale a 25/100.

• 1,75 pode ser representado como 1 75/100.

Esse tipo de fração é chamado de fração decimal.

Ela é muito comum em situações práticas, como medidas, preços e porcentagens. E por ser fácil de escrever com vírgula, é bastante usada no nosso dia a dia.

Leia também: Número elevado a zero: por que o resultado é sempre 1?

Como funcionam as operações com frações?

Agora que você já conhece os tipos de frações, fica mais fácil entender como funcionam as operações fracionárias. Elas podem ser: adição, subtração, divisão e multiplicação.

Confira como elas funcionam e assista aos exemplos nos vídeos do canal Estuda Mais, do YouTube!

Adição

Para somar frações que possuem o mesmo denominador, basta mantê-lo e somar os numeradores.

• Exemplo: 2/8 + 3/8 = 5/8

Para aprender como somar frações com denominadores diferentes, você vai precisar entender como funciona o MMC (mínimo múltiplo comum). Desta maneira, é possível igualar os denominadores e a partir daí fazer a adição.

• Exemplo: 1/6 + ¾

Neste caso, o MMC é 12. Você deve então dividi-lo por cada denominador e multiplicar tanto o denominador quanto o numerador por este número. Veja no exemplo:

12:6 = 2

1x2 / 6x2 = 2/12

12:4 = 3

3x3 / 4x3 = 9/12

Agora, com denominadores iguais, basta realizar a operação:

2/12 + 9/12 = 11/12

No vídeo abaixo você pode aprender com mais um exemplo de soma de frações com denominadores diferentes:

Subtração

Com a subtração acontece exatamente o mesmo que com a adição. Caso os denominadores sejam os mesmos, basta realizar a operação entre os numeradores e repetir o denominador.

• Exemplo: 5/7 - 3/7 = 2/7

Caso os denominadores sejam diferentes, precisamos realizar o mesmo processo que explicamos anteriormente. Primeiro, encontrar o MMC, igualar os denominadores, ajustar os numeradores e então fazer a operação.

• Exemplo: 5/7 – 3/5

Observe que neste caso, por se tratarem de números primos (ou seja, números naturais maiores que 1 divisíveis somente por eles mesmos e por 1), basta multiplicarmos um pelo outro para encontrarmos o MMC de 35.

5x5 / 7x5 = 25/35

3x7 / 5x7 = 21/35

Agora, com os denominadores igualados, basta fazer a subtração:

25/35 – 21/35 = 4/35

Que tal mais um exemplo? Aprenda com o vídeo abaixo como fazer uma subtração de frações com denominadores diferentes:

Multiplicação

Para multiplicar frações, basta multiplicar numerador por numerador e denominador por denominador.

• Exemplo: ¾ x 2/7 = 6/28

Ainda na dúvida? Confira no vídeo como multiplicar frações com exemplos:

Divisão

Agora que você já sabe como multiplicar uma fração, fica fácil entender como dividir a fração. 

Para isso, tudo o que você vai precisar fazer é manter a primeira como está e inverter o numerador e o denominador da segunda. Depois, é só fazer a multiplicação.

Exemplo: 3/5 : 4/7 = 3/5 x 7/4 = 21/20

Vamos a mais um exemplo? Assista no vídeo abaixo mais uma explicação sobre como dividir fração para que não fique dúvidas:

5 exercícios resolvidos sobre frações

Para fixar melhor o conteúdo, nada melhor do que colocar em prática o que você aprendeu. A seguir, veja 5 exercícios resolvidos sobre frações, com explicações passo a passo para você entender como aplicar os conceitos de forma simples e direta.

Exercício 1 (Enem 2021)

Antônio, Joaquim e José são sócios de uma empresa cujo capital é dividido, entre os três, em partes proporcionais a: 4, 6 e 6, respectivamente. Com a intenção de igualar a participação dos três sócios no capital da empresa, Antônio pretende adquirir uma fração do capital de cada um dos outros dois sócios.

A fração do capital de cada sócio que Antônio deverá adquirir é

a) 1/2

b) 1/3

c) 1/9

d) 2/3

e) 4/3

Alternativa correta: c) 1/9

Resolução:

O capital da empresa está dividido assim:

Antônio: 4 partes

Joaquim: 6 partes

José: 6 partes

Total: 16 partes

Para que todos tenham a mesma participação, cada um deve ter:

16 ÷ 3 = 16/3 partes

Antônio tem 4 partes e quer chegar a 16/3:

16/3 − 4 = 4/3 (ele precisa adquirir 4/3 de capital)

Se ele vai tirar a mesma fração (x) de Joaquim e José, que têm 6 partes cada, então:

6x + 6x = 4/3

12x = 4/3

x = 4/3 ÷ 12

x = 4/3 × 1/12

x = 4/36

x = 1/9

Ou seja, Antônio deve adquirir 1/9 do capital de cada um dos outros dois sócios.

Exercício 2 (Enem-2017)

Em uma cantina, o sucesso de vendas no verão são sucos preparados à base de polpa de frutas. Um dos sucos mais vendidos é o de morango com acerola, que é preparado com 2/3 de polpa de morango e 1/3 de polpa de acerola.

Para o comerciante, as polpas são vendidas em embalagens de igual volume. Atualmente, a embalagem da polpa de morango custa R$ 18,00 e a de acerola, R$ 14,70. Porém, está prevista uma alta no preço da embalagem da polpa de acerola no próximo mês, passando a custar R$ 15,30.

Para não aumentar o preço do suco, o comerciante negociou com o fornecedor uma redução no preço da embalagem da polpa de morango.

A redução, em real, no preço da embalagem da polpa de morango deverá ser de

a) 1,20

b) 0,90

c) 0,60

d) 0,40

e) 0,30

Alternativa correta: e) 0,30

Resolução:

O suco é preparado com:

• 2/3 de polpa de morango

• 1/3 de polpa de acerola

Preço atual das embalagens:

• Morango: R$ 18,00

• Acerola: R$ 14,70

Custo atual do suco:

2/3 × 18,00 = 12,00

1/3 × 14,70 = 4,90

Total: 12,00 + 4,90 = R$ 16,90

Novo preço da polpa de acerola: R$ 15,30

Novo custo da parte de acerola:

1/3 × 15,30 = 5,10

Para manter o suco a R$ 16,90, a parte de morango deve custar:

16,90 − 5,10 = R$ 11,80

Agora, para saber o novo valor da embalagem de morango:

2/3 × x = 11,80

x = 11,80 ÷ (2/3)

x = 11,80 × (3/2)

x = 17,70

Preço atual: R$ 18,00

Novo preço: R$ 17,70

Redução necessária: 18,00 − 17,70 = R$ 0,30

Exercício 3 (Enem-2016)

No tanque de um certo carro de passeio cabem até 50 L de combustível, e o rendimento médio deste carro na estrada é de 15 km/L de combustível. Ao sair para uma viagem de 600 km o motorista observou que o marcador de combustível estava exatamente sobre uma das marcas da escala divisória do marcador, conforme figura a seguir.

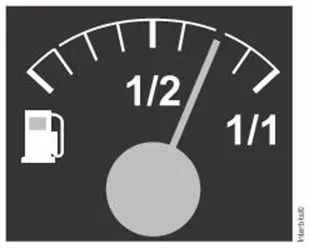
Como o motorista conhece o percurso, sabe que existem, até a chegada a seu destino, cinco postos de abastecimento de combustível, localizados a 150 km, 187 km, 450 km, 500 km e 570 km do ponto de partida. Qual a máxima distância, em quilômetros, que poderá percorrer até ser necessário reabastecer o veículo, de modo a não ficar sem combustível na estrada?

a) 570

b) 500

c) 450

d) 187

e) 150

Alternativa correta: b) 500

Resolução:

O marcador indica que foi gasto 1/4 do combustível.

Portanto, ainda restam 3/4 do tanque.

• Capacidade total do tanque: 50 litros

• Consumo do carro: 15 km por litro

Com o tanque cheio, o carro percorre:

50 × 15 = 750 km

Agora, vamos calcular 3/4 de 750 km:

3/4 × 750 = (3 × 750) ÷ 4 = 2250 ÷ 4 = 562,5 km

Ou seja, com o combustível restante, ainda é possível rodar 562,5 km. Logo, o último posto onde o motorista pode abastecer com segurança é o que está a 500 km.

Exercício 4 (Enem 2021)

Um jogo pedagógico é formado por cartas as quais está impressa uma fração em uma de suas faces. Cada jogador recebe quatro cartas e vence aquele que primeiro consegue ordenar crescentemente suas cartas pelas respectivas frações impressas. O vencedor foi o aluno que recebeu as cartas com as frações: 3/5, 1/4, 2/3 e 5/9.

A ordem que esse aluno apresentou foi

a) 1/4, 5/9, 3/5, 2/3

b) 1/4, 2/3, 3/5, 5/9

c) 2/3, 1/4, 3/5, 2/3

d) 5/9, 1/4, 3/5, 2/3

e) 2/3, 3/5, 1/4, 5/9

Alternativa correta: a) 1/4, 5/9, 3/5, 2/3

Resolução:

Vamos comparar as frações 3/5, 1/4, 2/3 e 5/9 para ordená-las do menor para o maior.

Primeiro, colocamos todas as frações com o mesmo denominador. O mínimo múltiplo comum entre 4, 5, 3 e 9 é 180. Convertendo as frações:

1/4 = 45/180

5/9 = 100/180

3/5 = 108/180

2/3 = 120/180

Agora é só comparar os numeradores:

45 < 100 < 108 < 120

Portanto, a ordem crescente das frações é:

1/4, 5/9, 3/5, ?

Exercício 5 (Enem Digital 2020)

É comum as cooperativas venderem seus produtos a diversos estabelecimentos. Uma cooperativa láctea destinou 4 m³ de leite, do total produzido, para análise em um laboratório da região, separados igualmente em 4000 embalagens de mesma capacidade.

Qual o volume de leite, em mililitro, contido em cada embalagem?

a) 0,1

b) 1,0

c) 10,0

d) 100,0

e) 1 000,0

Alternativa correta: e) 1 000,0

Resolução:

Volume total de leite:

4 m³ = 4 × 1.000.000 = 4.000.000 mililitros

Quantidade de embalagens:

4.000

Cálculo do volume por embalagem:

4.000.000 ÷ 4.000 = 1.000 mililitros

Cada embalagem contém 1.000,0 ml

Onde usar as frações no dia a dia?

A matemática está presente em todos os aspectos das nossas vidas — e isso inclui as frações. Mesmo sem perceber, usamos esse tipo de cálculo em várias situações cotidianas. Veja alguns exemplos:

• Culinária e receitas: ao seguir instruções como “meia xícara de leite” ou “1/4 de colher de sal”.

• Dinheiro e finanças: para calcular parcelas, dividir contas e entender juros ou descontos.

• Tempo e relógio: quando dizemos que passou “meia hora” ou “um quarto de hora”.

• Construção civil e medições: na medição de espaços, cortes de materiais ou proporções de mistura.

• Educação e notas escolares: ao calcular médias, porcentagens ou fracionar pontos de provas.

• Esportes e estatísticas: para analisar aproveitamentos, tempos de jogo ou frações de segundos.

• Descontos e promoções: como em liquidações de “1/2 do preço” ou “25% off”.

• Repartição de contas e recursos: ao dividir uma pizza, uma barra de chocolate ou um valor entre pessoas.

• Tempo e produtividade: para planejar tarefas, dividir períodos ou organizar rotinas.

Como o Kumon pode te ajudar a estudar frações?

Quando o aluno se matricula no curso de Matemática Kumon, ele tem o primeiro contato direto com o nosso método de ensino individualizado e respeitando as características de cada aluno.

Isso porque o aluno faz um teste, e cada um começa em um ponto diferente, de acordo com seu conhecimento sobre a matéria. 

Isto acontece em todas as disciplinas oferecidas pelo Kumon (Matemática, Português, Inglês e Japonês), mas é especialmente importante em matemática.

Por ser uma matéria que depende muito dos conhecimentos acumulados, quando o aluno não compreende um conceito, como números primos, divisão, multiplicação ou MMC, por exemplo, não consegue entender assuntos mais avançados, como frações.

Ou seja, ao começar em um ponto em que se sente seguro, o aluno do Kumon avança aos poucos e conforme entende cada tema, preparando o caminho para sua evolução. 

E o melhor: faz isso com segurança e motivação. É neste ponto que algo mágico acontece: o aluno passa a gostar de estudar matemática!

Se você quiser saber mais sobre nossa metodologia, acesse o site e veja todos os benefícios de estudar matemática pelo método Kumon.

Conclusão

Como você viu neste texto, aprender frações não é tão complicado quanto parece. Quando a gente entende a lógica por trás delas, fica muito mais fácil realizar operações e enxergar seu papel dentro da matemática.

Sabendo que as frações servem para representar partes de um todo, dá pra entender melhor como somar, subtrair, multiplicar e dividir esse tipo de número.

Além de ser um conhecimento super útil no dia a dia — afinal, nem sempre lidamos com números inteiros —, as frações também ajudam a desenvolver o raciocínio lógico matemático.

E se você ainda acha que frações não fazem parte da sua rotina, que tal prestar um pouco mais de atenção ao seu redor? Um desconto de 25% no seu game favorito, por exemplo, nada mais é do que tirar ¼ do valor.

Viu só? Entender os tipos de frações e como elas funcionam vai te ajudar não só a estudar para prova, mas também na forma como você observa o mundo e lida com ele.

Se ainda estiver com dúvidas, aproveite e confira estas 14 dicas de como aprender matemática do zero. E sempre que quiser ir além nos estudos, pode contar com o Kumon!